Trees

A tree is a data structure that simulates a hierarchical tree, with a root value and the children as the subtrees, represented by a set of linked nodes. The children of each node could be accessed by traversing the tree until the specified value is reached.

This is a non-linear data structure unlike the other types of data structures like arrays, stacks and queues.

Basic Terminology

Before exploring trees, we need to learn of the basic terminologies associated with them:

Root: The first node in a tree is called as Root Node. Every tree must have one Root Node.

Parent Node: The node which is a predecessor of any node is called a Parent Node, that is, the node which has a branch from it to any other node is called as the Parent node.

Child Node: The node which is descendant of any node is called as Child Node. Any parent node can have any number of child nodes. All the nodes except root are child nodes.

Siblings: Nodes which belong to the same Parent are called as Siblings.

Leaf Node: In a tree data structure, the node which does not have a child is called a Leaf Node. They are also known as External Nodes or Terminal Nodes.

Internal Nodes: The node which has at least one child is called an Internal Node.

External Nodes: The node which has no child is called an External Node.

Degree: The total number of children of a node is called a Degree of that Node. The highest degree of a node among all the nodes in a tree is called the Degree of the tree.

Level: In a tree, each step from top to bottom is called a Level.

Height: The total number of edges from the leaf node to a particular node in the longest path is called as Height of that Node.

Depth: The total number of edges from the root node to a particular node is called the Depth of that Node.

Path: The sequence of Nodes and Edges from one node to another node is called a Path.

Types of a tree

There are multiple types of trees with their various properties:

1. General trees
2. Binary trees
3. Binary Search trees
4. M-way trees
5. AVL trees

General Tree

A general tree is a tree where each node may have zero or more children. The other types of trees are special cases of general trees.

Mathematically it can be defined as a finite non-empty set of elements. One of these elements is called the root and the remaining elements when partitioned into trees, are called the subtrees of the root.

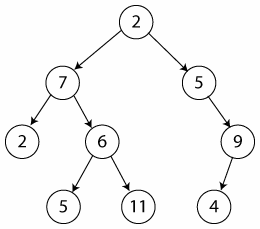
Binary Tree

In a normal tree, each node can have any number of children. A Binary tree is a special case of general tree in which every node can have a maximum of two children. One is known as the left child and the other as right child.

Binary Search Trees

A Binary Search Tree is a binary tree that additionally satisfies the binary search property. This tree is used to decreases the number of comparisons to be made in the tree to find an element, like a regular binary search.

The binary search property states that the key in each node must be greater than or equal to any key stored in the left sub-tree, and less than or equal to any key stored in the right sub-tree.

Multiway Trees

A multiway tree can have more than one value per node. They are written as m-way trees where m means the order of the tree. A multiway tree can have m-1 values per node and m children. It is not necessary that every node has m-1 values or m children.

The 2 most used variants of multiway trees are:

1. B-Trees

A B-tree is a specialized M-way tree that is widely used for disk access. A B tree of order m can have a maximum of m–1 keys and m pointers to its sub-trees.

It was developed in the year 1972 by Bayer and McCreight. A B-tree is designed to store sorted data and allows search, insertion, and deletion operations to be performed in logarithmic running time.

2. B+ Trees

A B+ tree can be viewed as a B-tree in which each node contains only keys (not key-value pairs), and it stores all the records at the leaf level of the tree instead.

AVL trees

An AVL tree is a self-balancing binary search tree . A binary tree is said to be balanced, if the difference between the heights of left and right subtrees of every node in the tree is either -1, 0 or +1.

Applications of Trees in Programming

• File System structure: The directories and subdirectories of a file system are efficiently be represented by a tree structure. 
• DOM structure: HTML pages are rendered using a DOM structure which contains all the tags used in the page. This is a tree-like structure. 
• Router algorithms: Router algorithms construct a tree of the locations across the network to determine the route that data packets must follow to reach their destination efficiently.

Continue Reading

• Tree Traversals: Read about the various tree traversal algorithms.
• Binary Trees: Read about the binary tree.
• Binary Search Trees: Read about the binary search tree.
• Multiway Trees: Read about the multiway tree.
• AVL Trees: Read about the AVL tree.